অর্থের বর্তমান মূল্য ও বিনিয়ােগ সিদ্ধান্তের পারস্পরিক নির্ভরশীলতা
মাধ্যমিক ও উচ্চ শিক্ষা অধিদপ্তর ২০২১ সালের এসএসসি পরীক্ষায় অংশগ্রহণ করতে ইচ্ছুক শিক্ষার্থীদের চতুর্থ সপ্তাহের অ্যাসাইনমেন্ট প্রকাশ করেছেন। ব্যবসায় শিক্ষা বিভাগ থেকে ২০২১ সালের এসএসসি পরীক্ষায় অংশগ্রহণকারী শিক্ষার্থীদের এই সপ্তাহে ফিন্যান্স ও ব্যাংকিং পাঠ্যবই তৃতীয় অধ্যায়: অর্থের সময় মূল্য থেকে অর্থের বর্তমান মূল্য ও বিনিয়ােগ সিদ্ধান্তের পারস্পরিক নির্ভরশীলতা সংক্রান্ত একটি নির্ধারিত কাজ দেয়া হয়েছে।
জাতীয় শিক্ষাক্রম ও পাঠ্যপুস্তক বোর্ড এনসিটিবি কর্তৃক প্রণীত এসএসসি ২০২১ এর সকল বিষয়ের সংক্ষিপ্ত সিলেবাস এর আলোকে প্রণীত ১২ সপ্তাহের অ্যাসাইনমেন্ট এর মধ্যে চতুর্থ সপ্তাহে ব্যবসায় শিক্ষা বিভাগের শিক্ষার্থীদের জন্য ফিন্যান্স ও ব্যাংকিং বিষয় এটি তৃতীয় এসাইনমেন্ট।
এসএসসি পরীক্ষা ২০২১ চতুর্থ সপ্তাহের অ্যাসাইনমেন্ট ফিন্যান্স ও ব্যাংকিং
২০২১ সালের এসএসসি পরীক্ষার্থীদের চতুর্থ সপ্তাহে ব্যবসায় শিক্ষা বিভাগের শিক্ষার্থীদের ফিন্যান্স ও ব্যাংকিং বিষয়ের তৃতীয় এসাইনমেন্ট নেয়া হয়েছে পাঠ্য বইয়ের তৃতীয় অধ্যায়: অর্থের সময় মূল্য থেকে। এসএসসি ২০২১ ফিন্যান্স ও ব্যাংকিং চতুর্থ সপ্তাহের অ্যাসাইনমেন্ট সম্পন্ন করতে গিয়ে শিক্ষার্থীদের পাঁচটি প্রশ্নের উত্তর দিতে হবে। উত্তর লেখার পারদর্শিতার ওপর নির্ভর করে মূল্যায়ন প্রক্রিয়া অনুযায়ী বিষয় শিক্ষকগণ সর্বোচ্চ ১৬ নম্বর পর্যন্ত প্রদান করবেন।
চতুর্থ সপ্তাহে এসএসসি পরীক্ষার্থীদের ফিন্যান্স ও ব্যাংকিং বিষয় এর এসাইনমেন্ট সমাধান করতে গিয়ে শিক্ষার্থীরা অর্থের বর্তমান মূল্য ও ভবিষ্যৎ। মূল্যের মধ্যে সম্পর্ক নির্ণয় করতে পারবে অর্থের বর্তমান মূল্য নির্ণয় করে। বিনিয়ােগ সিদ্ধান্ত নিতে পারবে।
নিচের ছবিতে ২০২১ সালের এসএসসি পরীক্ষার্থীদের ব্যবসায় শিক্ষা বিভাগের ফিন্যান্স ও ব্যাংকিং তৃতীয় এসাইনমেন্ট বিস্তারিত উল্লেখ করা হলো

শ্রেণিঃ এসএসসি ২০২১, বিভাগঃ ব্যবসায় শিক্ষা, বিষয়ঃ ফিন্যান্স ও ব্যাংকিং, অ্যাসাইনমেন্ট নং-০৩, অধ্যায় ও শিরোনামঃ তৃতীয় অধ্যায়: অর্থের সময় মূল্য
অ্যাসাইনমেন্টঃ অর্থের বর্তমান মূল্য ও বিনিয়ােগ সিদ্ধান্তের পারস্পরিক নির্ভরশীলতা বিশ্লেষণ
নির্দেশনা (সংকেত/ধাপ/পরিধি): অ্যাসাইনমেন্ট প্রণয়নের ক্ষেত্রে নিম্নের বিষয়গুলাের যথাযথ ব্যাখ্যা ও নির্ধারিত সমস্যার যথাযথ সমাধান বিবেচনায় নিতে হবে –
উদাহরণসহ অর্থের বর্তমান মূল্য ও বার্ষিক বাট্টাকরণ প্রক্রিয়ার ব্যাখ্যা উদাহরণসহ বছরে একাধিকবার বাট্টাকরণের মাধ্যমে বর্তমান মূল্য নির্ণয়ের প্রক্রিয়া ব্যাখ্যা;
সমস্যা:
নিরাপদ লিমিটেড ৩ বছর পর ১৫ লক্ষ টাকার মেশিন ক্রয়ের উদ্দেশ্যে এখনই প্রয়ােজনীয় অর্থ ব্যাংকে বিনিয়ােগ করতে ইচ্ছুক। ‘অভয়’ ব্যাংক ১০% বার্ষিক চক্রবৃদ্ধি মুনাফা দিবে এবং উদয় ব্যাংক ৯.৫০% ত্রৈমাসিক চক্রবৃদ্ধি মুনাফা দিবে। প্রতিষ্ঠানটি অর্থ বিনিয়ােগের জন্য যে কোনাে একটি ব্যাংক নির্বাচন করতে চায়।
অর্থের বর্তমান মূল্য ও বিনিয়ােগ সিদ্ধান্তের পারস্পরিক নির্ভরশীলতার ভিত্তিতে দুটি ব্যাংকের মধ্যে কোনটিতে বিনিয়ােগ করা যৌক্তিক হবে তা বিশ্লেষণ করতে হবে।
নির্দেশকঃ
ক) অর্থের বর্তমান মূল্য ও বাট্টাকরণ প্রক্রিয়া;
খ) বার্ষিক বাট্টাকরণ ও বছরে একাধিক বাট্টাকরণ;
গ) বার্ষিক বাট্টাকরণ ও বছরে একাধিক বাট্টাকরণ করে অর্থের বর্তমান মূল্য নির্ণয়;
ঘ) অর্থের বর্তমান মূল্য ও বিনিয়ােগ সিদ্ধান্তের পারস্পরিক নির্ভরশীলতা;
এসএসসি পরীক্ষা ২০২১ চতুর্থ সপ্তাহের ফিন্যান্স ও ব্যাংকিং অ্যাসাইনমেন্ট সমাধান ও উত্তর
২০২১ সালের এসএসসি পরীক্ষার্থীদের চতুর্থ সপ্তাহে ফিন্যান্স ও ব্যাংকিং অ্যাসাইনমেন্ট পেপার এ উল্লেখিত নির্দেশনা ও মূল্যায়ন রুবিক্স সমূহ যথাযথভাবে অনুসরণ করেন শিক্ষার্থীদের জন্য একটি নমুনা উত্তর প্রস্তুত করে দেওয়া হল।
এসএসসি পরীক্ষার ২০২১ সালের চতুর্থ সপ্তাহের ফিন্যান্স ও ব্যাংকিং বিষয়ে অ্যাসাইনমেন্ট এর নমুনা উত্তর অনুসরণ করে শিক্ষার্থীরা অ্যাসাইনমেন্টে দেওয়া প্রশ্নগুলোর যথাযথ উত্তর লিখতে পারবে এবং মূল্যায়নে সর্বোচ্চ নম্বর পাবে।
(উত্তর শুরু)
অর্থের বর্তমান মূল্য ও বিনিয়ােগ সিদ্ধান্তের পারস্পরিক নির্ভরশীলতা
ভূমিকাঃ ভবিষ্যতের একটি নির্দিষ্ট পরিমাণে টাকা বাট্টাকরণের মাধ্যমে আজকের বর্তমান মূল্য কত তা নির্ণয় করাকে অর্থের বর্তমান মূল্য বলে সময়ের পরিবর্তন একক নগদ প্রবাহের বর্তমান মূল্যকে হ্রাস করবে। আজকের ১০০ টাকার ক্রয়ক্ষমতা ১ বছর পরের ১০০ টাকার ক্রয়ক্ষমতা এক নয়। এর মূল কারণ হলো অর্থের সময়মূল্য বা সুদের হার। তাই সময় যত বৃদ্ধি পাবে একক নগদ প্রবাহের বর্তমান মূল্যও তত হ্রাস পাবে।
সময় ও সুদের হারের কারণে বর্তমান মূল্য ও ভবিষ্যৎ মূল্যের মাঝে পার্থক্যের সৃষ্টি হয়। সময় যতই বাড়তে থাকে ভবিষ্যৎ মূল্য ততই বাড়তে থাকে। আবার সুদের হার বেশি হলে ভবিষ্যৎ মূল্যও বেশি হয়। ফলে বর্তমান মূল্য ও ভবিষ্যৎ মূল্যের মধ্যে পার্থক্যের সৃষ্টি হয়। এ ছাড়া চক্রবৃদ্ধি সংখ্যার কারণেও বর্তমান মূল্য ও ভবিষ্যৎ মূল্যের মধ্যে পার্থক্যের সৃষ্টি হয়।
ফিন্যান্সের দৃষ্টিতে সময়ের সাথে সাথে অর্থের মূল্য পরিবর্তিত হয় অর্থাৎ এখনকার ৫০ টাকা আর পাচঁ বছর পরের ৫০ টাকা সমান মূল্য বহন করে না। এখন কার ৫০ টাকা অধিকতর মূল্যবান। এটাই অর্থের সময় মূল্যের ধারণা। মনে করি,আমি আমার বন্ধুর কাছে ৫০ টাকা পাই।
এমতাবস্থায় আমার বন্ধু বললাে এখন সে ৫০ টাকা পরিশােধ না করে ১ বছর পর পরিশােধ করবে। অর্থের সময় মূল্য বলে যে,এখনকার ৫০ টাকা আর এক বছর পরের ৫০ টাকা সমান মন বহন করে না।
অর্থের ভবিষ্যৎ মূল্য ও চক্রবৃদ্ধিকরণ প্রক্রিয়াঃ
বর্তমান মূল্য জানা থাকলে ১নং সূত্র ব্যবহার করে ভবিষ্যৎ মূল্য বের করা যায়। বাসরিক মেয়াদ সূত্র -১: ভবিষ্যৎ মূল্য (FV) = বর্তমান মূল্য (১+ সুদের হার) এখানে FV হচ্ছে Future Value বর্তমানের ১০০ টাকার ১ বছর পরের ভবিষ্যৎ মূল্য = ১০০ (১+০.১০) = ১০০ x ১.১০ = ১১০ টাকা বর্তমানের ১০০ টাকার ২ বছর পরের ভবিষ্যৎ মূল্য = ১০০ (১+০.১০) = ১০০ X ১.২১ = ১২১ টাকা;
ভবিষ্যৎ মূল্য নির্ধারণের জন্য উপরিউক্ত উদাহরণে যে প্রক্রিয়াটি ব্যবহৃত হয়েছে, তাকে বলা হয় চক্রবৃদ্ধিকরণ পদ্ধতি। এখানে লক্ষণীয় যে এক বছর পরে ১১০ টাকা ভবিষ্যৎ মূল্যের মধ্যে আসল ১০০ টাকা ও সুদ ১০ % হারে ১০ টাকা।
একই ভাবে দ্বিতীয় বছর আরও ১০ টাকা সুদ হলে দ্বিতীয় বছরে ভবিষ্যৎ মূল্য হওয়া উচিত ১২০ টাকা কিন্তু দ্বিতীয় বছরের ভবিষ্যৎ মূল্য হয়েছে ১২১ টাকা এর কারণ দ্বিতীয় বছরের শুরুতে আসল ধরা হয় ১১০ টাকা এবং তাতে করে দ্বিতীয় বছরে ১০ % হারে সুদ হয় ১১ টাকা।
বার্ষিক চক্রবৃদ্ধিকরণ ও বছরে একাধিক চক্রবৃদ্ধিকরণ করে অর্থের ভবিষ্যৎ মূল্য নির্ণয়ঃ
কখনাে কখনাে বছরে একাধিকবার চক্রবৃদ্ধি হতে পারে। যেমন: ব্যাংকে টাকা রাখলে মাসিক ভিত্তিতে চক্রবৃদ্ধি হয়। অর্থাৎ বছরে ১২ বার চক্রবৃদ্ধি হয়। সেক্ষেত্রে সূত্রটিতে দুটি পরিবর্তন করতে হবে। বছরে যদি বারবার চক্রবৃদ্ধি হয়, তাহলে প্রথমত সুদের হারকে ১২ দিয়ে ভাগ করতে হবে এবং দ্বিতীয়ত মেয়াদকেও ১২দিয়ে গুণ করতে হবে। একটি উদাহরণের মাধ্যমে সূত্রটির প্রয়ােগ দেখানাে হলাে।
উদাহরণ-৩: যদি তুমি ১০% চক্রবৃদ্ধি সুদে ১০০ টাকা ব্যাংকে জমা রাখ এবং তুমি জানাে বছরে ১২ বার চক্রবৃদ্ধি হবে, তবে ১ বছর পর তুমি কত টাকা পাবে? এর সমাধানের জন্য তােমাকে নিচের সূত্রটি ব্যবহার করতে হবে-
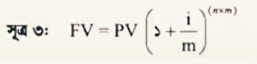
এখানে, বর্তমান মূল্য (PV) = ১০০ টাকা, সুদের হার (i) = ১০%, বছরে চক্রবৃদ্ধির সংখ্যা (m) = ১২, বছরের সংখ্যা (n) = ১ বছর, ভবিষ্যৎ মূল্য (FV) =?
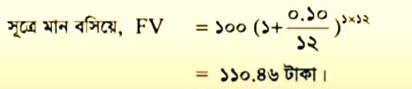
ধারণা: যদি তুমি আজকে ১০০ টাকা ব্যাংকে জমা রাখ তাহলে ১ বছর পরে তুমি ১১০.৪৬ টাকা পাবে। | অর্থাৎ তুমি ১১০.৪৬ – ১০০ = ১০.৪৬ টাকা বেশি পাবে।
বিনিয়োগ সিদ্ধান্ত গ্রহণ
বিনিয়োগ সিদ্ধান গ্রহণ করার জন্য উভয় ব্যাংকের কার্যকরী সুদের হার নির্ণয় করতে হবে।
x ব্যাংকের কার্যকরী সুদের হার,
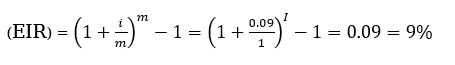
এখানে, m= বছরে চক্রবৃদ্ধির সংখ্যা = ১, i = বার্ষিক সুদের হার = ৯%
Y ব্যাংকের কার্যকরী সুদের হার,
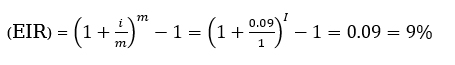
এখানে, m= বছরে চক্রবৃদ্ধির সংখ্যা = ৫২, i = বার্ষিক সুদের হার = ৮.৫০%
বিনিয়োগে পরামর্শ: x ব্যাংকে ৬ লক্ষ এবং Y ব্যাংকে ৪ লক্ষ টাকা রাখলে তিনি অধিক লাভবান হবেন।
অর্থের ভবিষ্যৎ মূল্য ও চক্রবৃদ্ধিকরণ প্রক্রিয়াঃ
বর্তমান মূল্য জানা থাকলে ১নং সূত্র ব্যবহার করে ভবিষ্যৎ মূল্য বের করা যায়। বাসরিক মেয়াদ সূত্র -১: ভবিষ্যৎ মূল্য (FV) = বর্তমান মূল্য (১+ সুদের হার) এখানে FV হচ্ছে Future Value বর্তমানের ১০০ টাকার ১ বছর পরের ভবিষ্যৎ মূল্য = ১০০ (১+০.১০) = ১০০ x ১.১০ = ১১০ টাকা বর্তমানের ১০০ টাকার ২ বছর পরের ভবিষ্যৎ মূল্য = ১০০ (১+০.১০) = ১০০ X ১.২১ = ১২১ টাকা;
ভবিষ্যৎ মূল্য নির্ধারণের জন্য উপরিউক্ত উদাহরণে যে প্রক্রিয়াটি ব্যবহৃত হয়েছে, তাকে বলা হয় চক্রবৃদ্ধিকরণ পদ্ধতি।
এখানে লক্ষণীয় যে এক বছর পরে ১১০ টাকা ভবিষ্যৎ মূল্যের মধ্যে আসল ১০০ টাকা ও সুদ ১০ % হারে ১০ টাকা।
একই ভাবে দ্বিতীয় বছর আরও ১০ টাকা সুদ হলে দ্বিতীয় বছরে ভবিষ্যৎ মূল্য হওয়া উচিত ১২০ টাকা কিন্তু দ্বিতীয় বছরের ভবিষ্যৎ মূল্য হয়েছে ১২১ টাকা এর কারণ দ্বিতীয় বছরের শুরুতে আসল ধরা হয় ১১০ টাকা এবং তাতে করে দ্বিতীয় বছরে ১০ % হারে সুদ হয় ১১ টাকা।
উদাহরণ ৩: জনাব মিজান আজকে সােনলী ব্যাংকের সঞ্চয়ী হিসাবে শতকরা ১০% হার সুদে ৫,০০০ টাকা জমা রেখেছে। ১ম বছর, ২য় বছর এবং ৩য় বছর শেষে সে কত টাকা ফেরত পাবে?
সমাধানঃ
আমরা জানি, ভবিষ্যত মূল্য (Fv) = P (1+i) n
এখানে, বর্তমান মূল্য (P) = ৫,০০০, এ সুদের হার (i) = ১০%, সময় বা মেয়াদকাল (a) =১,২ ও ৩ বছর;
ভবিষ্যত মূল্য (FV) = ?
১ বছর পরের ভবিষ্যৎ মূল্য (FV) = P(1+i)”
= ৫,০০০ (১+0,১০)১ = ৫,০০০x১.১০ = ৫,৫০০ টাকা।
২ বছর পরের ভবিষ্যৎ মূল্য (Fv) = pv (I+i)n
= ৫,০০০ (১+০.১০)২ = ৫,০০০x১.২১ = ৬০৫০ টাকা।
৩ বছর পরের ভবিষ্যৎ মূল্য (FV) = P(1+i)”
= ৫,০০০ (১+০.১০)৩ = ৫,০০০x১.৩৩ = ৬,৬৫৫ টাকা।
বছরে একাধিকবার চক্রবৃদ্ধিকরণের ক্ষেত্রে ভবিষ্যৎ মূল্য নির্ণয় প্রক্রিয়া:
চক্রবৃদ্ধিকরণ এর ক্ষেত্রে বার্ষিক চক্রবৃদ্ধি এবং বছরে একাধিকবার চক্রবৃদ্ধিকরণের মাধ্যমে ভবিষ্যৎ মূল্য হিসাব করা যায়। বছরে একাধিকবার চক্রবৃদ্ধিকরণের ক্ষেত্রে ভবিষ্যৎ মূল্য নির্ণয় এর সূত্রে M ব্যবহার করতে হয়।
যেখানে প্রতিমাসে চক্রবৃদ্ধির ক্ষেত্রে M এর মান 12, দ্বিমাসিক চক্রবৃদ্ধির ক্ষেত্রে M এর মান 6, ত্রৈমাসিক চক্রবৃদ্ধির ক্ষেত্রে M এর মান 4, সপ্তাহিক চক্রবৃদ্ধি ক্ষেত্রে এর মান 52 ধরা হয়।
যেমন, যদি কোন ব্যাংকে 1000 টাকা 5 বছরের জন্য জমা রাখা হয় এবং ব্যাংক যদি 10% হারে মাসিক চক্রবৃদ্ধি প্রদান করে তবে পাঁচ বছর পরে মূল্য হবে,
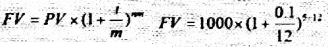
FV =1000×1.6453, FV = 1645.3 টাকা (প্রায়)
বিনিয়ােগ সিদ্ধান্ত গ্রহণ:
আমরা জানি, বার্ষিক চক্রবৃদ্ধি ক্ষেত্রে ভবিষ্যৎ মূল্য, (কোন কিছু উল্লেখ না থাকলে বার্ষিক) FV = Pvx(1+)”
এখানে, X ব্যাংকের ক্ষেত্রে বর্তমান মূল্য PV= 600000 টাকা,
বার্ষিক চক্রবৃদ্ধি সুদের হার = 9% বা 0:09, বছর সংখ্যা n= 5 বছর ভবিষ্যৎ মূল্য = ?
FV = 600000x (1+ 0.09) FV = 600000×1.5386 FV =923160 টাকা (প্রায়)


এক্ষেত্রে পাঁচ বছর পর মােট পাবেন =615440+917460=1532900 টাকা (প্রায়) সিদ্ধান্তঃ যেহেতু প্রথম অবস্থার ক্ষেত্রে পাঁচ বছর পরে মােট মূল্য অপেক্ষা দ্বিতীয় অবস্থার ক্ষেত্রে পাঁচ বছর পরে মােট মূল্য কম, সেহেতু প্রথম অবস্থাতে অর্থাৎ X ব্যাংকে 6 লক্ষ টাকা এবং Y ব্যাংকে ৭ লক্ষ টাকা জমা রাখলে তিনি অধিক লাভবান হবেন।
বন্ধুরা এই ছিল তোমাদের জন্য এসএসসি পরীক্ষা ২০২১ চতুর্থ সপ্তাহের ফিন্যান্স ও ব্যাংকিং অ্যাসাইনমেন্ট সমাধান ও উত্তর অর্থের বর্তমান মূল্য ও বিনিয়ােগ সিদ্ধান্তের পারস্পরিক নির্ভরশীলতা
উত্তরটি প্রদান করেছে শাহিদা আক্তার, কুমিল্লা ভিক্টোরিয়ার সরকারি কলেজ, কুমিল্লা;
প্রতি সপ্তাহে সকল স্তরের অ্যাসাইনমেন্ট সংক্রান্ত সকল তথ্য পাওয়ার জন্য বাংলা নোটিশ এর ফেসবুক পেজটি লাইক এবং ফলো করে রাখুন ইউটিউব চ্যানেল সাবস্ক্রাইব করে রাখুন এবং প্লেস্টোর থেকে অ্যান্ড্রয়েড অ্যাপটি ডাউনলোড করে রাখুন।
এসএসসি পরীক্ষা ২০২১ চতুর্থ সপ্তাহের সকল অ্যাসাইনমেন্ট এর সমাধান
চতুর্থ সপ্তাহে বিজ্ঞান, মানবিক ও ব্যবসায় শিক্ষা শাখার এসএসসি পরীক্ষার্থীদের সবগুলো বিষয় অ্যাসাইনমেন্ট এর প্রশ্ন বাছাই করার নমুনা উত্তর দেখার জন্য কাঙ্ক্ষিত বিষয়ে পাশে থাকা লাল বাটনে ক্লিক করুন-
[ninja_tables id=”10339″]